Chaining, and Cognitive Load

How can we manage the intrinsic cognitive load of chaining atoms?

Podcast is AI generated. Interactive transcript available here.

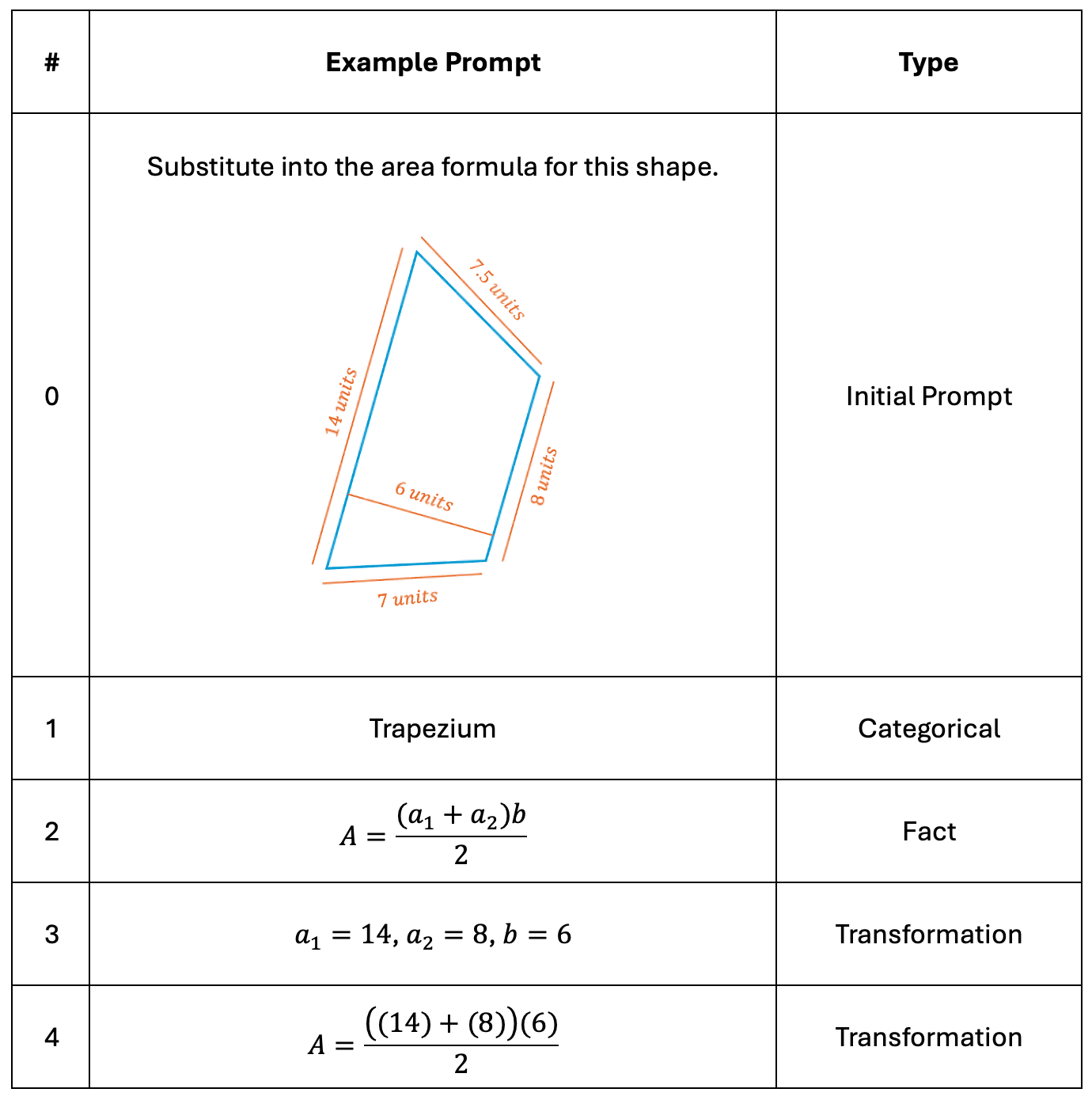
We’re trying to teach every single child in our class how to find the area of a trapezium. We’re not making any excuses - no matter the set, we’re aiming for 100%. We want them to be able to do this using the formula, and we want them to find the area even when redundant information is presented.

So far, we have atomised the routine:

We’re assuming that atoms 1 and 4-6 are all prior knowledge that has been mastered. We’re now assuming we’ve just taught atoms 2 and 3 and students have now mastered those too. What’s next?

What’s next is chaining.

Chaining is the process of putting the atoms back together into a step by step routine.

Now, students are learning what to do from start to finish, in order.

Importantly, this is now the only thing they are learning to do. Each individual atom has been learned, it is only the step by step routine from start to finish that is new.

Each step implies the next, which helps a lot with memory:

(1) If you’ve been asked to find the area and you’ve identified it’s a trapezium, then that implies you need the trapezium formula ((2) - which you’ve already memorised.)

(2) Once you’ve written down the formula, that implies you need to identify lengths a1, a2, and b ((3) - which you have previously mastered.)

(3) Once you have noted those three lengths, that implies substitution. (4)

(4) Once you have substituted, that implies calculation. (5)

(5) Once you have calculated, the fact that this is measuring an area implies the need for units. (6)

So this should be easy.

But it isn’t.

Because that’s still six atoms you have to recall from memory, along with the correct sequence, along with all the necessary processing along the way. If working memory capacity is around 3-4 ‘items,’ we’re still at risk of being well over the limits.

It depends on the class.

Once atom 3 is mastered, that’s it, some students will now race through the routine. Dead easy.

Others will still struggle, get stuck, get lost, forget what to do next, feel uncertain.

They’re the ones we need to find an answer for.

The answer is sub-chaining.

Sub-chaining asks students to process a smaller part of the whole chain, instead of the whole thing. For example:

This asks students to substitute into the formula, and stop there. No need to perform any calculations.

Here is a different sub-chain:

This one starts students at the end of atom 3, where the three values they need have been identified, and then asks them to substitute those values into the formula and work out the area with correct units.

In each case there are fewer atoms to process, reducing the cognitive load of the activity.

Later, the sub-chains can be extended, either joined together to form the full chain, or extended by just one atom, just one extra piece of work they have to do themselves.

This is also where worked-example problem pairs become most useful again. You can demonstrate the sub-chain end to end as an ‘I do,’ then on the right side of the board present a new, similar example for the students to attempt.

So, practising sub-chains before attempting the full chain is one way to further manage the cognitive load associated with learning a cognitive routine.

Another way is through overtisation. We’ll take a look at that in the next post.