Concrete Example - Teaching Bearings (1)

How have other teachers applied the Unstoppable Learning system to teaching bearings?

Podcast is AI generated, and will make mistakes. Interactive transcript available in the podcast post.

---

This is the first in a major series that this Substack was created for.

We’ve found that the teachers love the system, and it all seems simple enough, but then they sometimes run into problems when trying to apply it the first few times. Often it depends on the specific topic they have chosen and its idiosyncrasies, and usually results from an incomplete picture of the whole system.

Without support, this can lead teachers to return whatever traditional resources are at hand, and feeling they were somehow to blame, somehow unable to get it right.

Usually it’s more the case that there were tiny adjustments that might have made improvements. Also, even ‘imperfect’ design will often prove very effective.

By showing you how serving teachers are applying the system across a range of topics, along with our analyses and feedback, we hope to encourage the many of you working on this in your classrooms to keep trying, and offer some small support. We will even include cases where we suggest changes that might be improvements, but the teacher delivered their original design and still achieved a 100% success rate; proof that you don’t need to make perfect the enemy of good enough.

Our first topic is bearings.

If the goal is to teach ‘what a bearing is,’ then this is a categorical concept (you can meaningfully ask ‘is this a bearing?’) How to design the instructional sequence for categoricals is explained in this post:

How to Teach Element 1 of 4: Categoricals

Coincidentally, teachers in two schools were working on this at around the same time, while in the last podcast episode, Craig and Lee were also discussing Lee’s application of the system to teaching children ‘what is a bearing?’ (Around 1h09m.)

Our first example is courtesy of Sean Kirby at Pool Academy, part of the Athena Learning Trust.

Later in the week we will look at a second example, with thanks to Matt Dryden and Erin Thomson, at Lasswade Highschool, up in Scotland.

---

Sean shared this after just a couple of weeks of working together, very near the start.

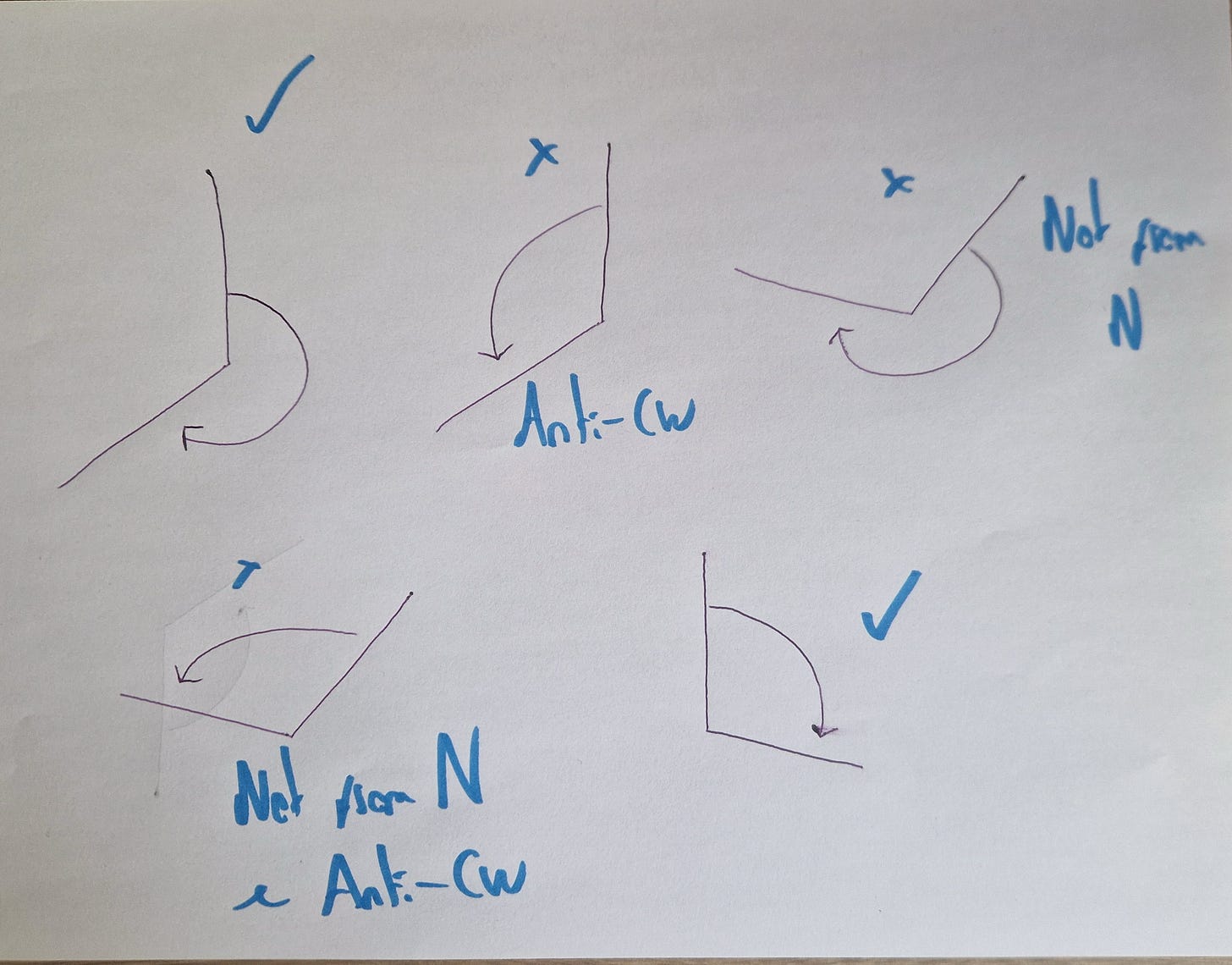
Read this top row first, left to right, and the bottom row.

Straight away you can see that the examples are adhering to the setup principle, all of the irrelevant features are held constant: basically the examples all look very similar, and change only in ways that matter, direction of measurement and measurement from north.

Also when moving from the first example to the second, you can see that it’s a very small change: the direction of measurement was clockwise, so that was an example of a bearing:

Then, the direction of measurement was anti-clockwise, so no longer an example of a bearing, even though everything else was the same.

This adheres to the difference principle (minimal differences between positives and negatives show the limits of a concept.)

There are also probably just enough examples to communicate the concept. Five examples is probably about right; not too many, not too few.

So already this is a strong design, and if it were tested in a classroom, it will probably work for most if not all students.

Our Analysis and Suggestions

We thought of a few ways this sequence can be tightened up that will increase the odds of success for 100% of students.

So here are our suggestions, along with the alternative sequence we recommended: