Podcast is AI generated, and will make mistakes. Interactive transcript available in the podcast post.
When in Year 10 Jacob was asked for the name of this shape:
He couldn’t say, even though he knew a five-sided shape was called a pentagon. Even after he counted the sides, he asked, unsure ‘Sir, is it a pentagon?’
Being ‘told’ the definition of a pentagon didn’t help him fluently identify pentagons. Words alone cannot communicate categorical and transformation concepts; that’s why we must develop instructional sequences to communicate them.
Using language to teach can fail in many ways.
However, so too can not using language.
Following an instructional sequence, my Year 7 nurture group of six, highly statemented students could now effortless identify prisms versus non-prims. 100% accuracy, every time. Easy.
However, ask them to put it into words, and not one of them could.
Two teachers we worked with on our Transformation Programme earlier this year, one in Liverpool, one in Scotland, used a categorical sequence to help their students identify angles in parallel lines: corresponding, alternate, co-interior.
Unprompted then, like me with my Year 7s, they each independently asked their students ‘so can you tell them then, what are corresponding angles?’
No-one gave the answer they were both looking for (same side of the transversal, and both either above or below the parallel lines.)
One or two in each class did offer a similar descriptive answer about ‘angles pointing the same direction.’
But as with my Year 7s, the reality is that neither group in either part of the UK knew how to talk about corresponding angles, even though they could easily say whether angles were corresponding or not.
I know what it means, I just don’t know how to say it
Now, you know what this feels like.
Remember the last time you used a slightly unusual word and someone asked you what it meant, and you took a breath, held it, realised you had no idea how to put it into words, then said something like ‘I know what it means, I just can’t put it into words.’ You probably then looked it up, and instantly remarked ‘yes! Exactly that, that’s what I was thinking’… even though, you weren’t really thinking it at all (if you were, you would have said it.)
This happens because we develop implicit knowledge without the explicit knowledge. These terms are essentially identical to the two related memory systems: implicit memory and explicit memory.
Implicit and explicit knowledge are related but distinct, and we can know one without the other.
Jacob had explicit knowledge of pentagons, but very limited implicit knowledge.
Whereas, my Year 7s had solid implicit knowledge of prisms, but no explicit knowledge of them. Same for students with the angles in parallel lines examples. Same for you last time you used that word correctly but couldn’t explain its meaning.
Without implicit knowledge we cannot think and act fluently, accurately and effortlessly.
Without related explicit knowledge we cannot talk about what we understand implicitly.
Grammar Arguments
Arguments about whether or not primary school students should have to learn about fronted adverbials in English grammar happened because the focus and assessment was on teaching them the explicit knowledge, which is arguably not as useful in this instance as the implicit knowledge knowledge needed to use them. But the public arguments often felt superficial and difficult to resolve because, with a deep and recursive irony, teachers understood this distinction implicitly, but didn’t have the language of implicit and explicit knowledge to better articulate their concerns.
Solution
A solution to communicating both implicit and explicit knowledge simultaneously is the correlated-features sequence.
Think of it as an optional add-on to any instructional sequence.
It asks the question ‘how do you know?’ after each example. It either teaches a fact or rule about the concept up front, or through the sequence.
So going back to our early posts on teaching Categoricals and Transformations, the correlated-features add-on might look like this:
Categorical - Triangle
I’m going to teach you what we mean by the word triangle.
A triangle is a closed shape with three sides.
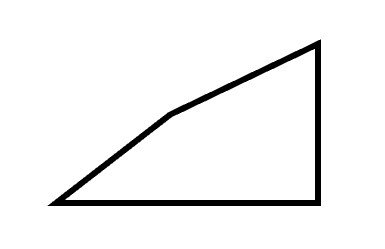
So for example, this is not a triangle.
How do I know?
Because it’s a closed shape, but it doesn’t have three sides.
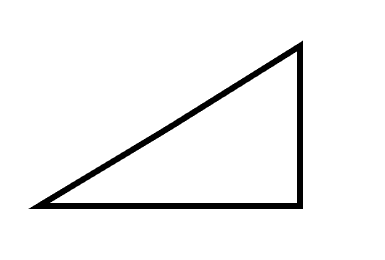
This is a triangle.
How do I know?
Because it’s a closed shape with three sides.
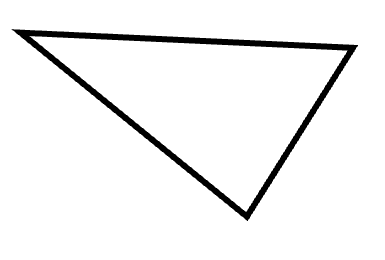
This is a triangle.
How do I know?
Because it’s a closed shape with three sides.
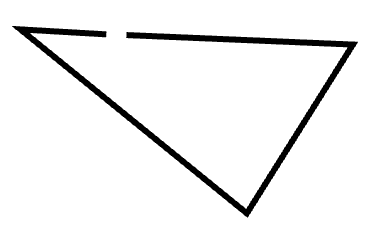
And this is a triangle.
How do I know?
Because it’s a closed shape with three sides.
But this is not a triangle.
How do I know?
Because it has three sides, but it’s not a closed shape.
Transformation - Writing Fractions Equal to 1
I’m going to show you how to write a fraction equal to 1.
Fractions are equal to 1 when their top and bottom are the same.
So for example, this:
Is now equal to one:
How do I know?
Because top and bottom are the same.
And this:
Is now equal to one:
How do I know?
Because top and bottom are the same.
Finally, this:
Is now equal to one:
How do I know?
Because top and bottom are the same.
In each example, the verbal rehearsal required to answer the question ‘How do I know?’ - or ‘How do you know?’ if directed to the students - both teaches students an explicit fact about the concept, and increases future recall.
Something like this might have worked for the corresponding angles in parallel lines example:
…how do I know?
Because they are on the same side of the transversal, and same side of the parallel lines.
But prism is a little trickier. We need the ends to the be the same polygon, same size, and same orientation, with no deviation from that along the length.
Correlated-features sequences, as a rule, shouldn’t try to communicate more than two features at once.
So in the future we’ll see how they could still be adapted and used to help teach explicit facts about prisms, but we’ll also look at an alternative approach that’s useful in this context, the fact system.