The Initial Testing Sequence
There are three instructional sequences: initial instruction, initial testing, and expansion. So far we have only looked at initial instruction. Now we will see initial testing.
Podcast is AI generated, and will make mistakes. Interactive transcript available in the podcast post.
Last time we looked at how to teach transformations:
Then we left off with 'well what now?’ Along with ‘yeah but did it really work? How do you know?’
To answer that, the teaching of categoricals and transformations can be split up into three parts; into three types of sequence:
Initial Instruction
Initial Testing
Expansion
Up to now, we have only presented initial instructional sequences.
When we discussed how to teach categoricals:
…again what we presented there was initial instruction only.
After initial instruction must come initial testing.
To be clear, you’re not testing the kids, you’re testing whether or not your communication was successful.
The Testing Principle
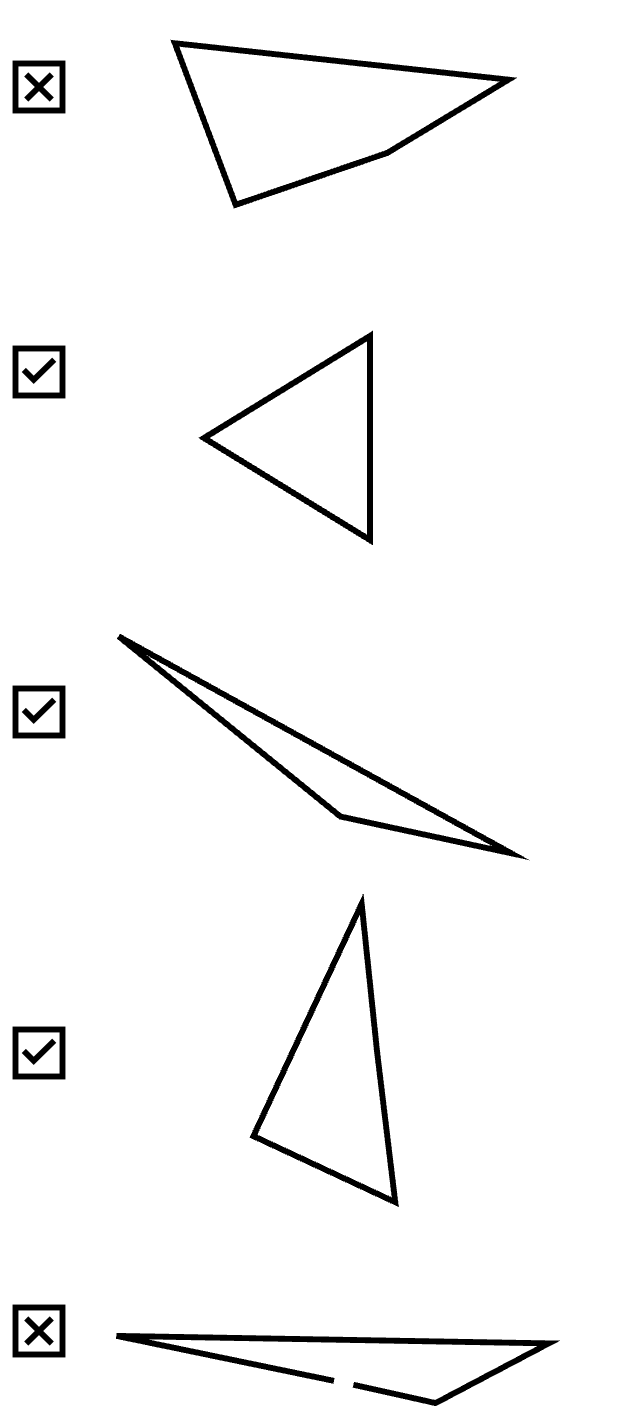
Say you delivered this categorical sequence for communicating what a triangle is:
Or this transformation sequence for communicating how to substitute:
Now you need to be sure that your communication was successful. To do this, a similar ‘testing sequence’ is offered. For categoricals that might be a sequence of 4-6 items. For transformations it might be a sequence of 4-6 items as well. Just enough to be sure the core concept was communicated before moving on to expansion.
For example, you could use choral response to have a whole class quickly respond to a sequence of questions like:
“Your turn. Is this a triangle?”
The items in the sequence should still have the same setup as during initial instruction.
But if you then worked through a sequence of examples like this one:
You would have just violated the testing principle.
The testing principle is straightforward: make sure that students cannot respond correctly by attending to the wrong thing (a spurious prompt.)
In this case, what might have gone wrong…?
Try comparing it to this alternative, which should work better:
The problem with the first option is that the pattern of correct responses precisely matches the initial instruction. A student could guess that the pattern of correct responses will again be NPPPN.
The testing principle is straightforward, but it is very easy to violate by mistake. For example, I once watched a lesson on finding the lowest common multiple in which two students were clearly paying no attention at all. Then the questions popped up on the board, and quick as a flash they picked up their mini whiteboards and had the correct response, they didn’t even need to list any of the multiples to work it out in their head.
How did they do it?
Well, the test item was this:
What is the lowest common multiple of 3 and 4?
They correctly responded with: 12.
So can they find the LCM of pairs of numbers?
Who knows. Most likely these two students, who’d paid no attention throughout, just saw two numbers on the board and multiplied them together.
Did they do that for sure? We’ll never know, because the testing principle has been violated. Maybe they did, maybe they didn’t.
The question should have been:
What is the lowest common multiple of 6 and 4?
That way we’d know. If they’re just multiplying the numbers, they’ll write 24. If they’re actually finding the LCM, they’ll write 12.
Next Time
Next week we will look at this in the context of I do / We do, and how it can go wrong, with thanks to Sianna Clarke, Head of Maths at Ilfracombe Academy in the Athena Learning Trust. When Sianna applied this model to teaching integration to an A Level class, it didn’t quite work out, and she had to return to a more traditional method for teaching the topic.
We’ll take a look at why, and in our analysis show what we could change to make the sequence work. Sianna’s example will be freely available, with our analyses and adjustments then made available to paying subscribers.