Which Atomisation is Better?
A different way to atomise finding the Nth Term Rule of a linear sequence. Is it better?
Podcast is AI generated, and will make mistakes. Interactive transcript available in the podcast post.
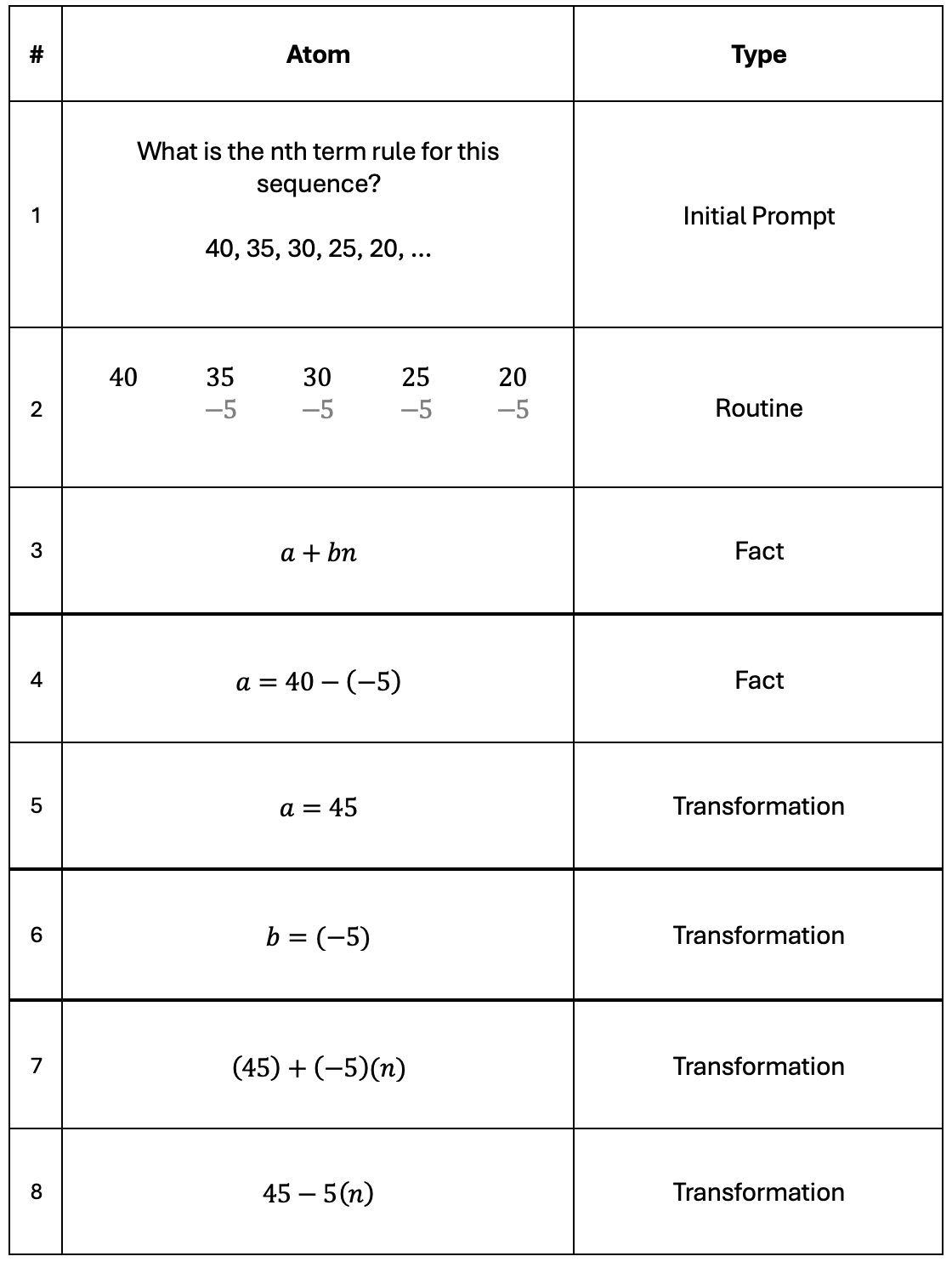
Last time I gave a step by step breakdown of how I atomised the process for finding the Nth Term Rule of a linear sequence, eventually settling on this:
has an alternative.First, I always think in terms of planning for the future. Is there a method I can teach them today that will still work as they continue to study higher level mathematics?
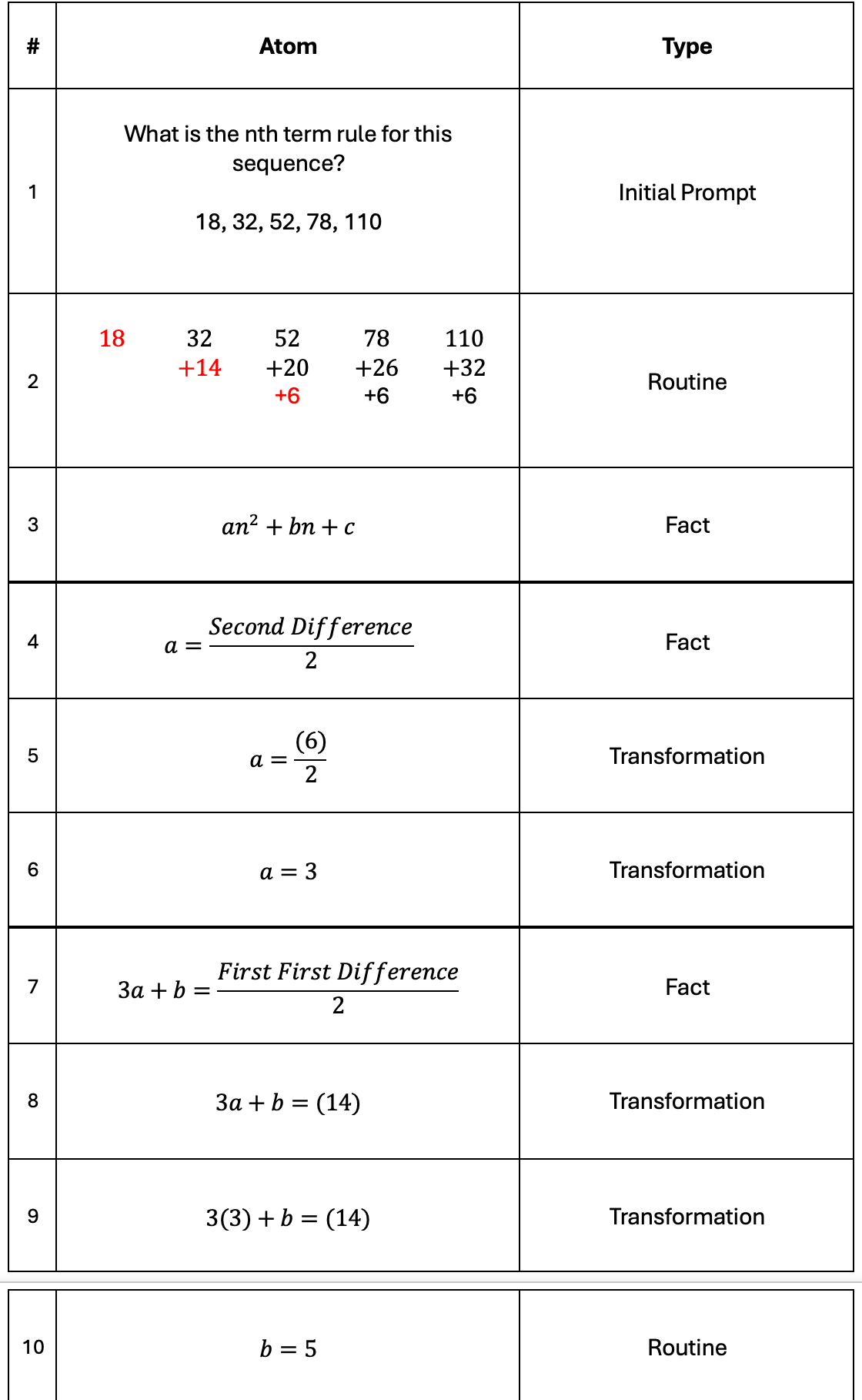
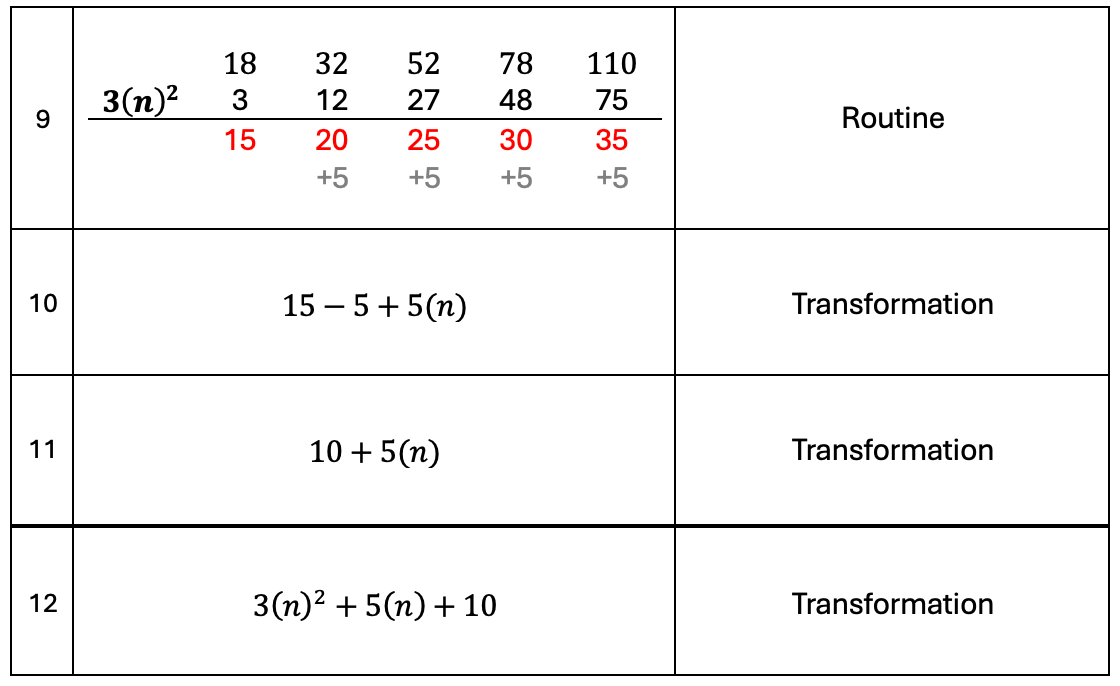
Finding the Nth term rule of a quadratic sequence is an obvious follow on, so how do you do that?
There are a few methods, but this is the approach I usually take:
This isn’t the easiest thing to learn.
It it has four facts you have to recall from memory.
You have to use three different parts of the sequence and its differences to find the three parameters (a, b, and c.)
You then have to substitute all three values into a general form for a quadratic.
It’s very easy to do, once you have learnt it - takes little time, very straightforward.
But it’s a pain to learn it all in the beginning, especially when it doesn’t connect well with many other parts of the later curriculum.
Unfortunately, there’s no way around it.
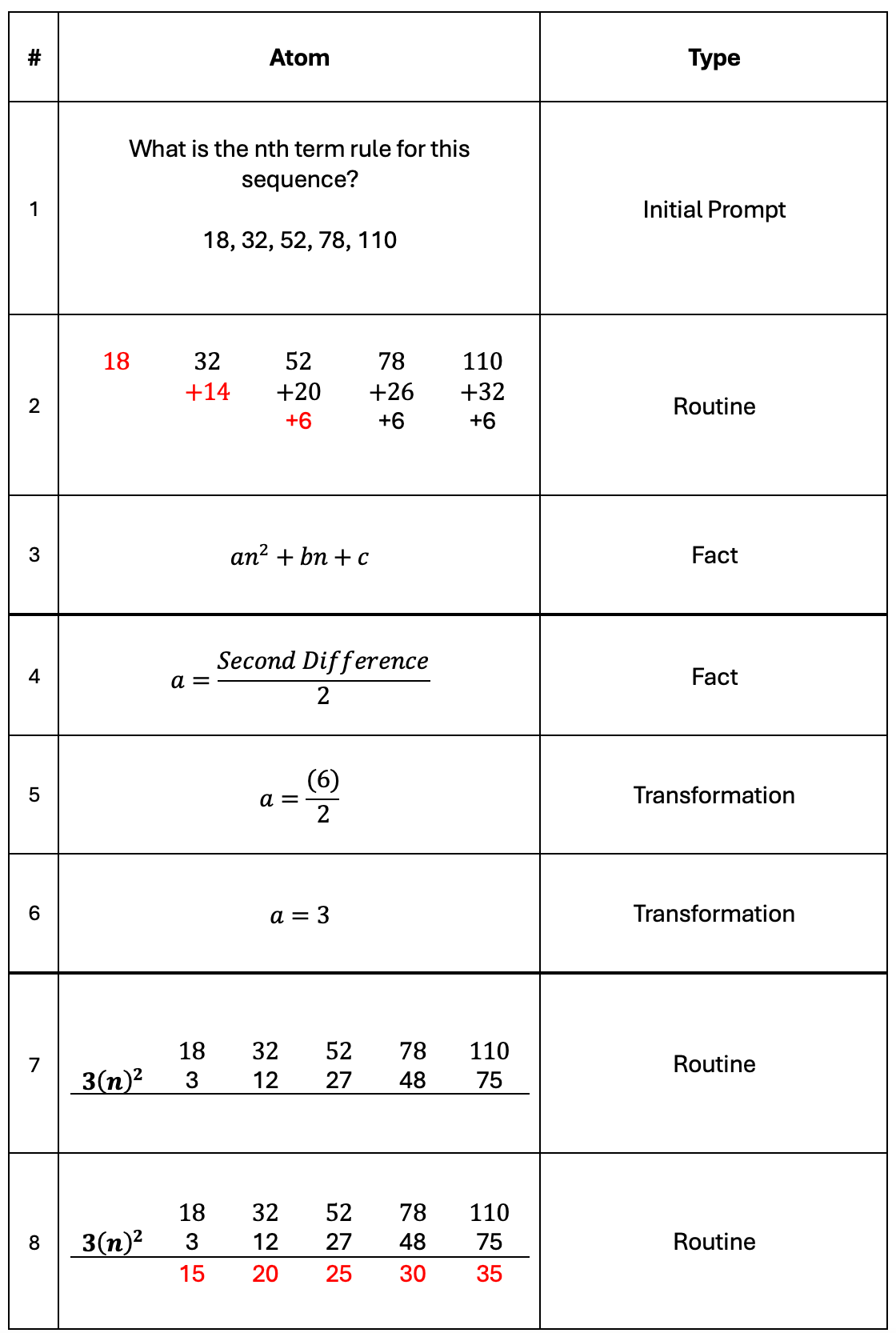
Other methods have their own problems. For example:
Just as much to remember, just as many steps, and many more subroutines in this atomisation, and in my experience kids get lost in the ever expanding tables of numbers of the subtraction method.
The rationale for why the subtraction method works isn’t any easier to follow than the rationale for the substitution method either.
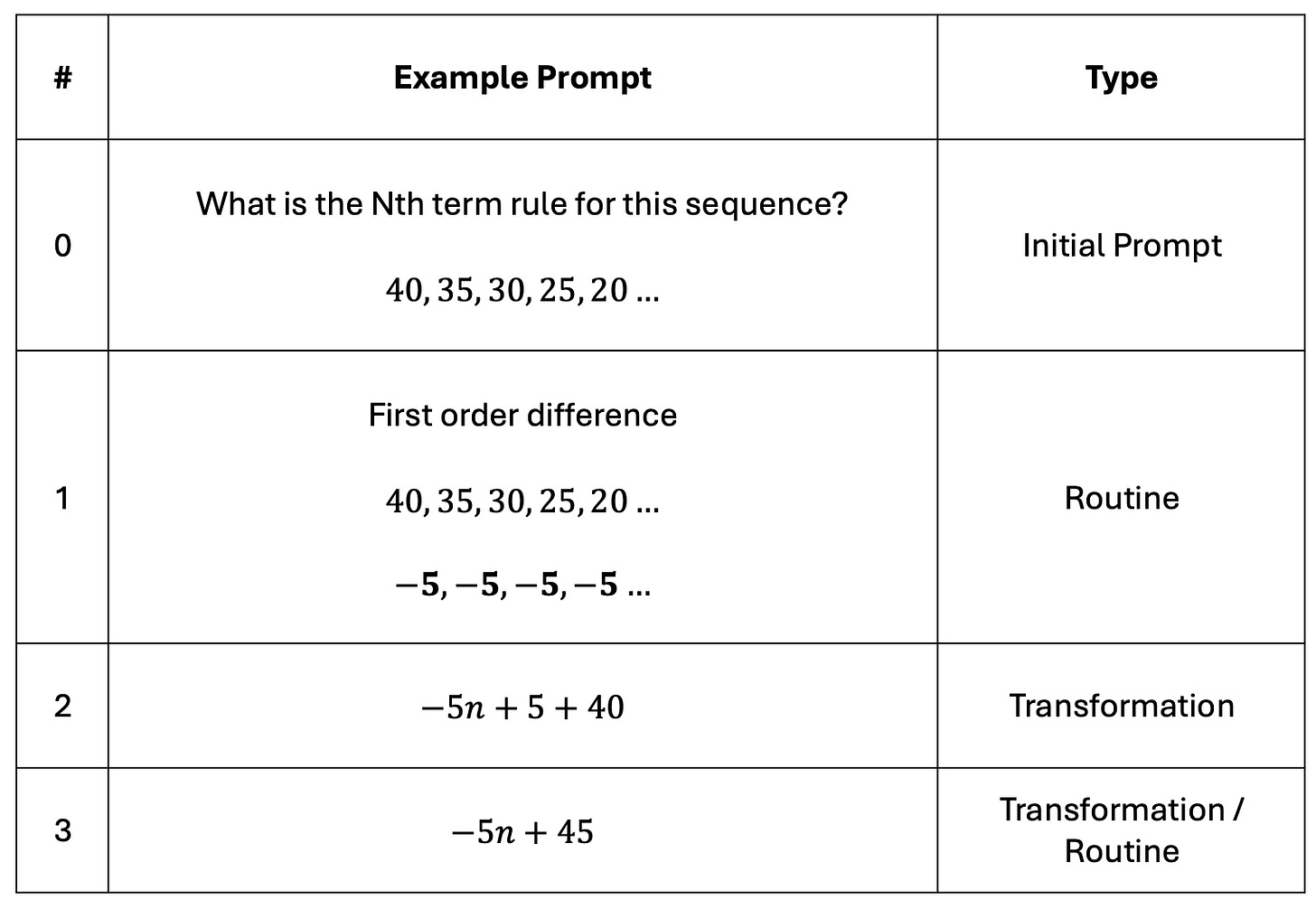
So then, for finding the Nth term rule of a linear sequence, I use an atomisation that involves a general form, finding parameters, and substitution.
I write the term in n second because it better maps to how students thing at first: they see us ‘starting with some constant’ and then ‘adding’ or ‘subtracting’ some amount each time.
I realise this is very similar to Kris’ first attempt here, which he ruled out:
I think the difference comes from Kris designing for a one off lesson, on linear sequences only, with a challenging class.
So time was constrained, student capability was constrained, and the learning objective was constrained accordingly - just get them to be able to easily, quickly, and accurately generate Nth term rules for linear sequences, including descending sequences starting with negative terms.
Whereas, I’m designing for the longterm, and am not imagining time as a constraint. I’m trying to teach students an idea that recurs throughout mathematics: that a model might have a parameterised general form, and if we know its general form, we now only need to find its parameters.
Kris and I agree that, while this approach is is more difficult to learn, even the bottom set could learn it. I think Kris also agrees that there might be a benefit to them learning this as the method, that it leads to a broader mathematical ability. But I’m not sure he’s convinced that it’s the best starting point as an introduction to finding the Nth term rule for any class. We’re still debating it.
What do you think? Which approach do you prefer, and why?
Comments below.


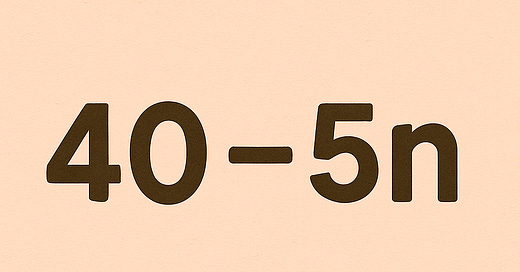




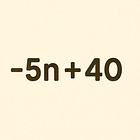

I have also been teaching in Australia and was planning to post something very similar to that Alex! Though your atomisation is a bit better than what I'd planned. I agree that there is no point teaching a skill very successfully in isolation if the skill is completely unrelated to all others. At its most extreme, I could teach this one this way: "The nth term of this sequence (...) is 40 - 5n. What is the nth term of this sequence?" Obviously this would be both successful - with sufficient retrieval practise - and utterly pointless as it wouldn't generalise to anything else and would be a useless fact connected to nothing else. On the other hand, I could go far the other way and include a check to see that it's linear, and make it more general - have a table of values in terms of x and y where x goes up in increments other than 1. Or where we're told its linear, but the x values goes up in irregular increments, and some process such as change in y over change in x, is required. This would then generalise completely to finding the equation of a straight line given a table of values.
Interesting Kris' point about the split attention effect and how a routine is better as one train of thought, I need to think about that more, seems useful.
There are three general principles I can think of when inventing a cognitive routine that need to be weighed up:
1) The more generalisable the routine is, the better. This relates to both the generalisability/usefulness of the atoms that need to be taught as well as the generalisability of the routine itself. Here, I agree that it should be a routine which clearly leads into understanding of linear relationships and graphing straight lines etc (as yours does Alex), as well as finding the nth term for quadratic sequences.
2) The more intuitive the routine is, the better. If steps make sense so that there are mechanisms for students to self check then that is better.
3) The simpler it is for students to learn, and the less time taken to teach and to do, the better.
Clearly, principle 1 is often in conflict with 2 and 3, and the desired generalisability is a function of many things.
For this specific case, I prefer the second approach you outline for finding the nth term of a quadratic sequence Naveen - atoms 9-11 should be a familiar subroutine and could simply be condensed to 'find nth term of resulting linear sequence' which should be secure by the time teaching this. In the first one, atom 7 is quite a useless fact in terms of generalisation of understanding and would be relatively hard to recall, its a shortcut to solving simultaneous equations (I also think maybe it shoudn't be divided by 2?) It might be simpler to learn, as principle 3 asks for, but is in conflict with both principle 1 and 2.
In terms of the nth term - I think a link to a linear sequence as in Alex's routine, increasing generalisability, is probably worth the hit to its intuitiveness. But maybe that's not the case given the GCSE syllabus.
Second thought:
Not many things have given me pause about the atomisation process since I've come across it. But I do worry about the lack of explicit teaching about conceptual generalisation at work here.
In this case, what a and b "do" for the sequence. I suppose the idea is that kids generalise themselves from examples? It just seems like a case where having a conceptual picture of what's going is helpful for internalising the steps (either a literal picture or some mechanical sense of how the rule generates the sequence).
But it seems like maths teaching is like political spin - if you're explaining you're losing?